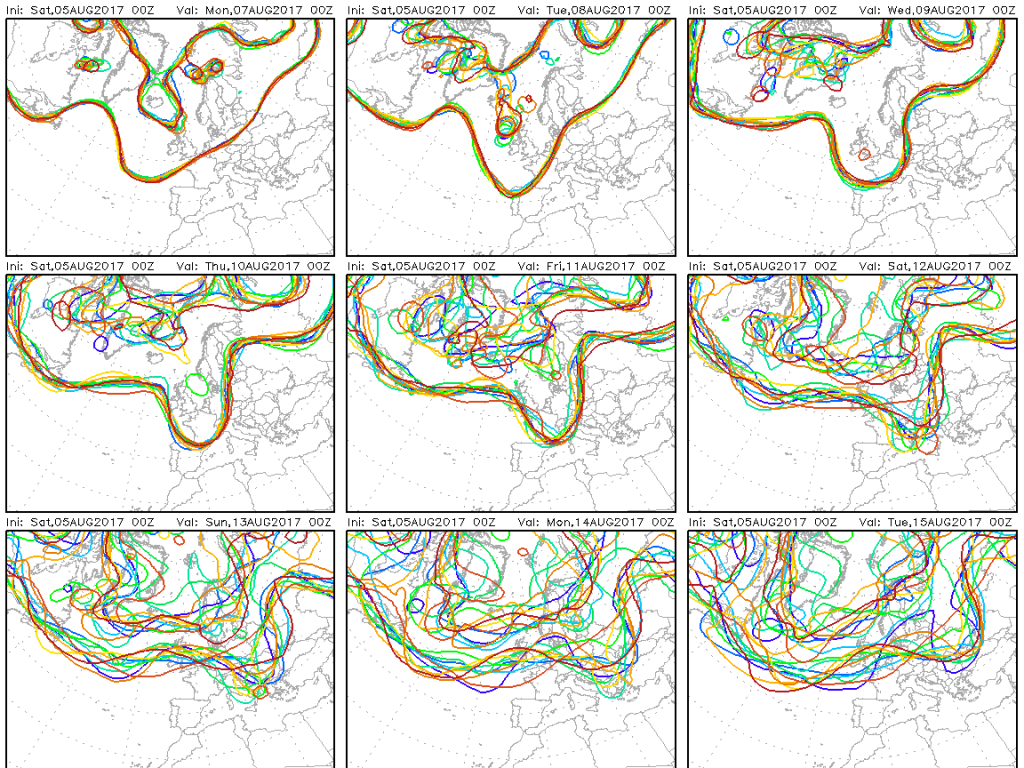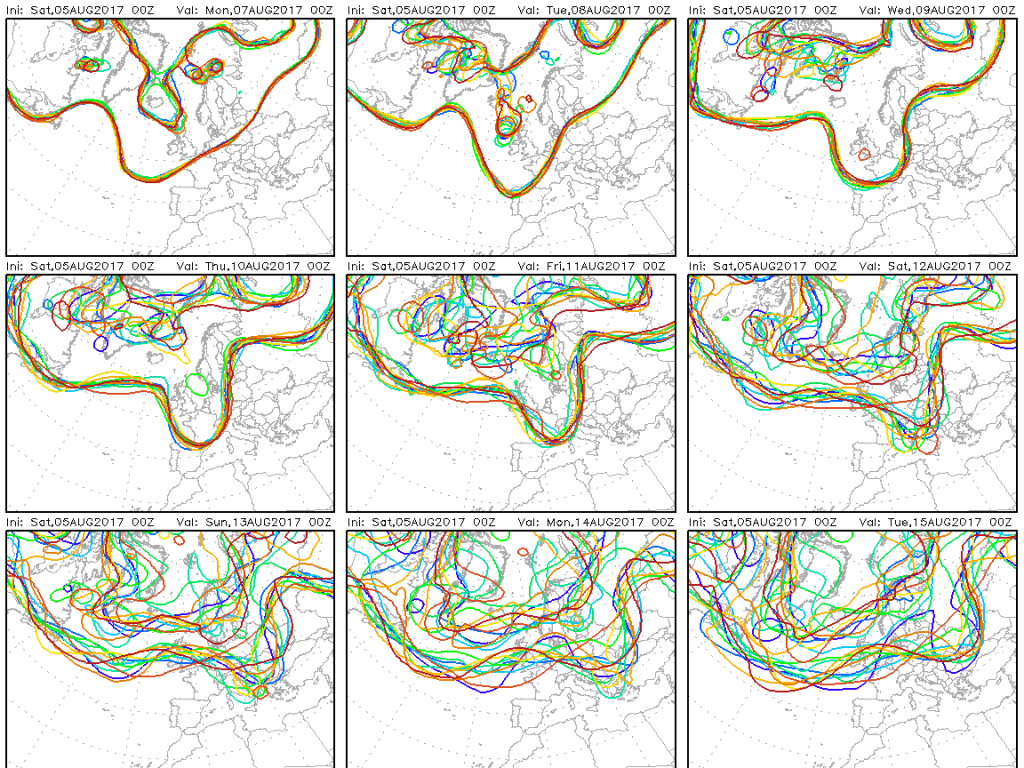
In molti dei miei articoli ma anche ascoltando le previsioni in tv, spesso rimandiamo alle mappe che i modelli previsionali, ci tratteggiano ad orari definiti. Oggi andiamo a spiegare come lavorano i modelli matematici, i correttivi che si applicano ma soprattutto l'incertezza che nonostante tutto ancora oggi delimita non poco l'affidabilità delle previsioni.
Un modello matematico, è un programma per computer che produce informazioni meteorologiche per momenti futuri a determinate posizioni e altitudini. Il dominio spaziale orizzontale di un modello è detto globale , se copre l'intero pianeta, regionale se copre solo una parte limitata del pianeta. I modelli regionali sono conosciuti anche come modelli di area limitata i (LAM) appunto.
Le previsioni vere e proprie, nascono usando equazioni differenziali matematiche per la fisica e la dinamica dell'atmosfera dette anche equazioni primitive dei moti atmosferici. Si tratta di equazioni non lineari, impossibili da risolvere esattamente cioè analiticamente. Perciò, i metodi utilizzati, propri dell'analisi numerica, ottengono soluzioni approssimate cioè con inevitabili errori. Modelli diversi utilizzano metodi numerici di soluzione diversi. Alcuni modelli globali usano metodi spettrali per le dimensioni orizzontali e metodi delle differenze finite per la dimensione verticale, mentre i modelli regionali e altri modelli globali usano metodi delle differenze finite in tutte e tre le dimensioni. I modelli regionali possono utilizzare anche griglie a risoluzioni spaziali più raffinate, per risolvere esplicitamente fenomeni meteorologici su scala più ridotta, in quanto non devono risolvere equazioni valide per l'intero globo potendo così sfruttare al massimo la potenza di calcolo del computer.
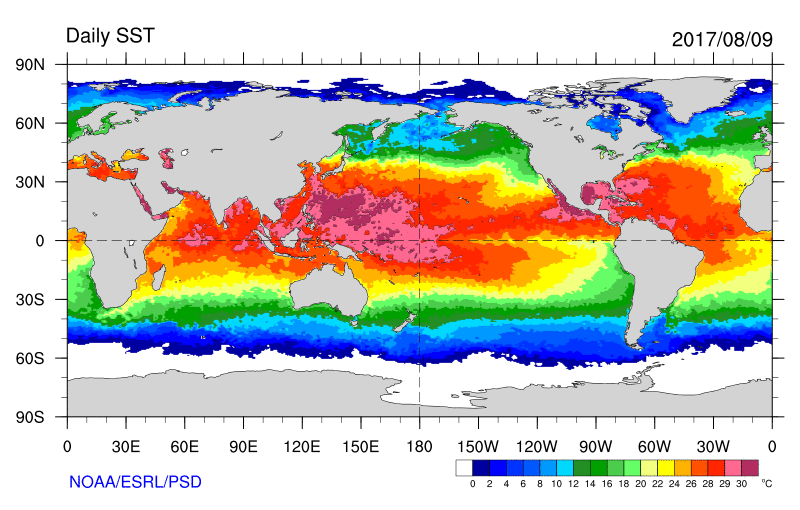
I modelli sono inizializzati usando dati osservati da radiosonde, satelliti meteorologici e osservazioni meteorologiche di superficie ovvero stazioni meteorologiche su terraferma e oceano (boe e navi). Le osservazioni, compiute su spaziature irregolari, sono elaborate mediante assimilazione di dati e metodi di analisi obiettivi, che effettuano il controllo di qualità e ricavano i valori presenti nelle località utilizzabili dagli algoritmi matematici del modello (di solito una griglia a spazi uniformi). I dati sono poi usati nel modello come punto di partenza per una previsione. Le equazioni primitive dei modelli sono inizializzate dall'analisi dei dati e sono determinati i tassi di variazione. Questi permettono di predire lo stato dell'atmosfera a un breve intervallo nel futuro.
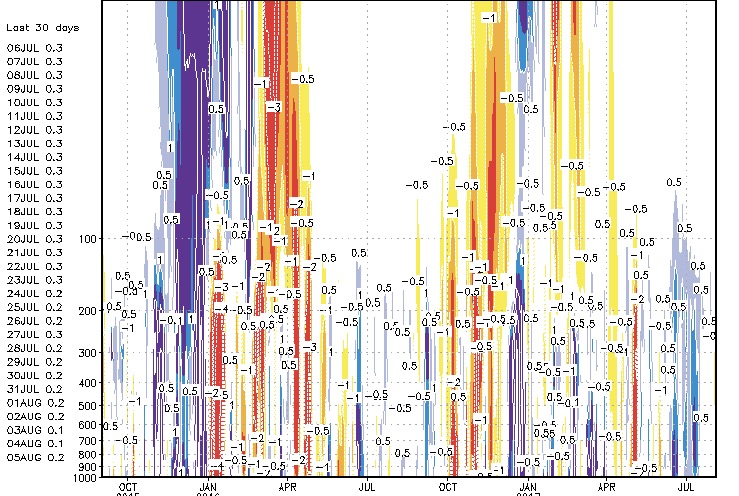
Questo nuovo stato atmosferico diviene il nuovo punto di partenza a cui sono applicate le equazioni per trovare nuovi tassi di variazione, che permettono a loro volta di predire lo stato atmosferico a un ulteriore intervallo nel futuro. Questa procedura per "passi temporali" è ripetuta continuamente finché la soluzione non raggiunge il momento desiderato della previsione. La lunghezza del passo temporale è collegata alla distanza tra i punti della griglia computazionale. I passi temporali per i modelli climatici globali possono essere dell'ordine di decine di minuti, mentre quelli per i modelli regionali possono oscillare da pochi secondi a pochi minuti. I risultati (output) dei modelli sono visualizzati su carte meteorologiche pronte all'uso per il meteorologo.
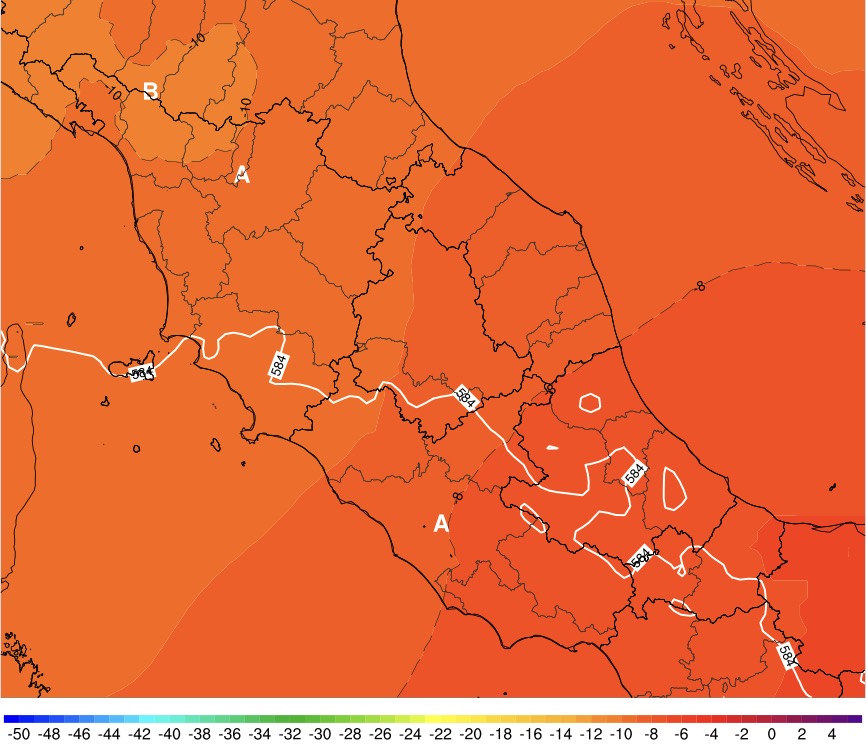
Come proposto da Edward Lorenz nel 1963, anche ammettendo di saper risolvere analiticamente le equazioni fondamentali dell'atmosfera (cosa non ancora raggiunta), è impossibile predire indefinitivamente (cioè deterministicamente una volta per tutte) lo stato dell'atmosfera a causa della natura non-lineare dunque caotica delle equazioni della dinamica dei fluidi che amplifica esponenzialmente l'inevitabile errore di inizializzazione del modello ovvero sulle condizioni iniziali. Come ulteriore fonte di incertezza si aggiunge il fatto che le reti di osservazione esistenti hanno una copertura o risoluzione spaziale limitata ovvero non omogenea, specialmente sulle grandi superfici d'acqua come l'Oceano Pacifico e l'emisfero meridionale, il che introduce maggiore incertezza sul reale stato iniziale dell'atmosfera.
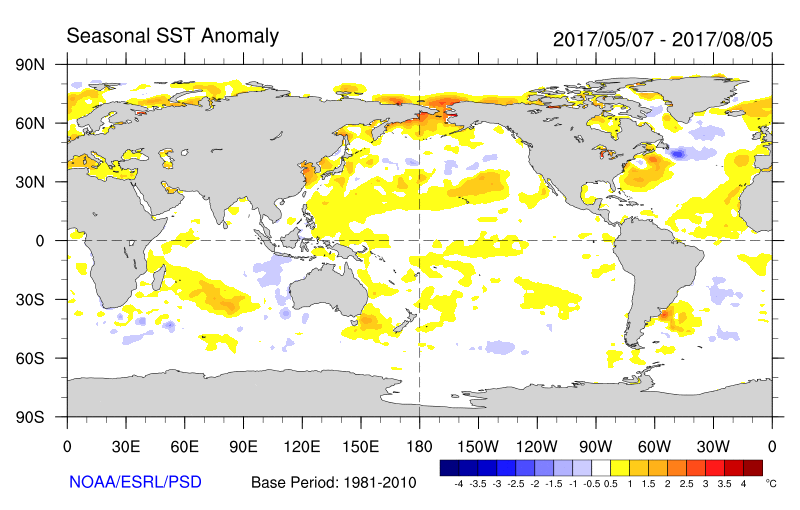
Attualmente il limite temporale massimo di predicibilità dello stato dell'atmosfera da parte di un qualunque modello numerico meteorologico è non superiore ai 15 giorni con un grado di affidabilità che decade nel tempo e varia anche in funzione del tipo di condizioni atmosferiche da prevedere. Al di sopra di questo limite si entra nel campo delle cosiddette, previsioni stagionali e dei relativi modelli, che giungono a coprire un arco temporale di 3-6 mesi basandosi però su principi fisici, considerazioni base e approcci diversi da quelli dei modelli meteorologici: l'idea di fondo è quella delle anomalie termiche oceaniche come forcing della circolazione atmosferica sotto forma di teleconnessioni atmosferiche e relative anomalie atmosferiche termiche, bariche e precipitative: essi hanno cioè una risoluzione spazio-temporale inferiore ai modelli meteorologici ovvero offrono una prognosi di semplice 'tendenza' risultando più simili ai modelli climatici e sono tuttora in fase di sperimentazione e sviluppo.
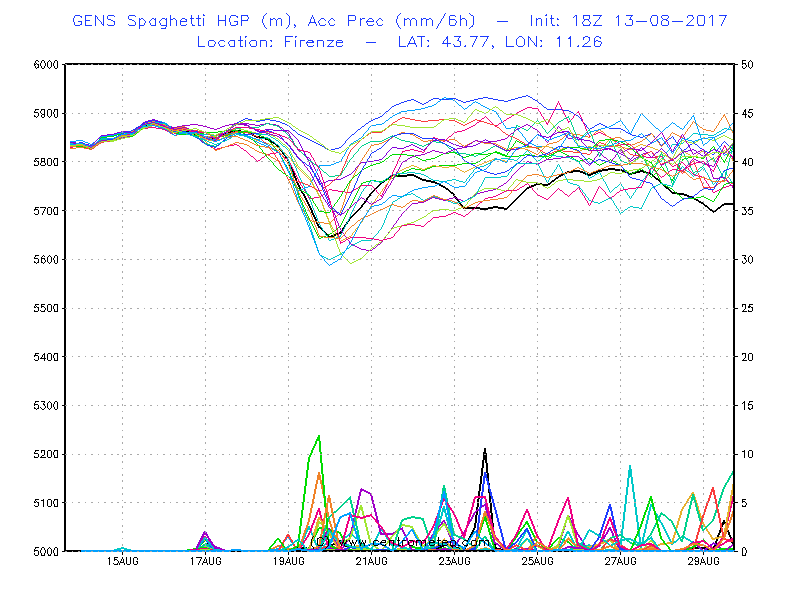
Per tenere conto dell'incertezza insita nei metodi e nei modelli di previsione, cercare di aumentarne l'affidabilità e al contempo spingere in avanti il limite di validità della previsione è attualmente in uso la cosiddetta previsione stocastica o "per insiemi" (ensemble forecasting), che implica previsioni multiple create o con uno stesso modello a partire da condizioni iniziali diverse, comprese all'interno di una certa gamma di valori possibili, o con gruppi di modelli diversi tra loro per diverse parametrizzazioni fisiche utilizzate (multimodel ensemble forecasting) oppure incrociando tra loro entrambi i metodi.
Solitamente, la previsione per insiemi è valutata in termini di media d'insieme (ossia la media pesata con la verosimiglianza della condizione iniziale oppure con la probabilità di successo del modello precedentemente valutata statisticamente) di una variabile previsionale, e del divario o ampiezza (spread) all'interno dell'insieme, che rappresenta il grado di accordo tra varie previsioni nel sistema degli insiemi, note come elementi dell'insieme. Un fraintendimento comune consiste nel credere che una bassa dispersione tra gli elementi dell'insieme implichi necessariamente un maggior grado di confidenza nella media dell'insieme. Sebbene a volte esista una relazione divario-attendibilità, la relazione tra il divario dell'insieme e il grado di attendibilità o capacità previsionale (forecast skill) varia in modo sostanziale in base a fattori quali il modello di previsione e la regione alla quale si applica la previsione.
Ecco perchè, di fronte alla mole di dati che possiamo avere a disposizione ogni giorno, non siamo ancora giunti ad unico utopico modello matematico che potrebbe in teoria garantire previsioni affidabili al 100% magari anche a medio termine. Discorso diverso invece andrebbe fatto per quei LAM (i modelli a corto raggio tipo i mesoscala , dove si analizzano moti atmosferici con lunghezze e caratteristiche che vanno da poche decine a poche centinaia di chilometri, come la circolazione atmosferica e le precipitazioni associate alle zone frontali, o eventi estremi come uragani o tempeste alle medie latitudini. Andando poi ancora più nel dettaglio, ci sarebbero anche quei modelli che analizzano i fenomeni anche in ambito ancora più ristretto detto microscala, e che riguarda moti ordini di lunghezza minori o uguali alla decina di chilometri. Su questa scala si osserva una vasta varietà di fenomeni, tra i quali i moti che portano alla formazione di nubi convettive, e le turbolenze che causano la dissipazione dell'energia cinetica dei moti di scala superiore.
Gordon Baldacci